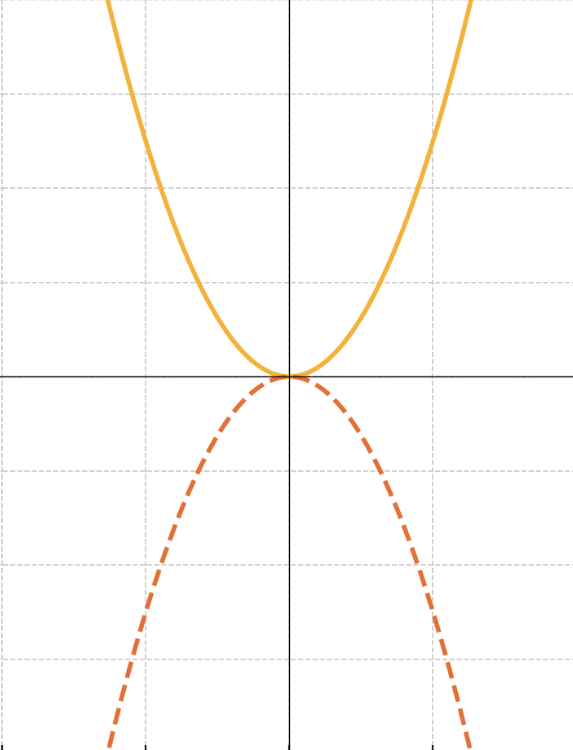
1. 放物線の「形」を理解する

二次関数のグラフは「放物線」という曲線を描きます。次の点を意識すると、お子さまに説明しやすくなります。

• 「上に開く」と「下に開く」: 二次関数の式 y = ax^2 で、係数 a が正のときは「上に開く」放物線、負のときは「下に開く」放物線になります。
• 「グラフの幅」: a の絶対値が大きいと（例：y = 3x^2）、グラフが細くなります。逆に絶対値が小さいと（例：y = 0.5x^2）、グラフが広がるイメージです。実際にいくつか異なる値でグラフを描いてみると、視覚的にわかりやすいのでおすすめです。

2. 頂点と軸の理解

放物線の「頂点」と「軸」について知っておくと、グラフの特徴を掴みやすくなります。

• 頂点: 放物線の一番上（または一番下）の点で、二次関数の特徴をつかむ重要な要素です。例えば y = x^2 - 4x + 3 の頂点は「グラフの中心」でもあります。
• 軸: 放物線の左右対称の線で、頂点を通る縦の線です。この軸を意識することで、グラフ全体の形がつかみやすくなります。

3. 重要な点を押さえてグラフを描く

実際にグラフを描いてみることで、放物線の形をより理解できます。以下の3点を押さえると、スムーズにグラフを描けるようになります。

• y切片: グラフがy軸と交わる点で、x = 0 のときの y の値です。例えば y = x^2 - 4x + 3 の場合、x = 0 のとき y = 3 になります。
• 軸と対称性: 頂点を通る軸を考え、左右対称な点を一対ずつ取ってグラフの形を描くと、きれいな放物線になります。
• 他の点の値: お子さまが自分でいくつかの x の値を入れて y の値を計算することで、点を取る練習になります。グラフに点を打ち、放物線の形を視覚的に確認しましょう。

おすすめのサポート方法

1. 計算手順を一緒に確認する

二次関数の計算はステップが多いので、計算手順を確認してあげると安心です。特に、間違いやすい計算（負の符号や分数など）を丁寧に確認することで、ミスを減らせます。

2. 問題を解く際に「なぜ」を考える

グラフや二次関数の計算結果を見て、「なぜこの結果になるのか」を一緒に考えると、理解が深まります。たとえば、「なぜグラフは上に開くのか？」といった視点で一緒に考えると、子ども自身が答えを見つけやすくなります。

3. 実生活に例える

放物線の形を現実の物に例えると、より身近に感じられます。たとえば、ボールを投げたときの軌跡や、橋のアーチの形が放物線に似ていると話してみると、理解が深まるかもしれません。

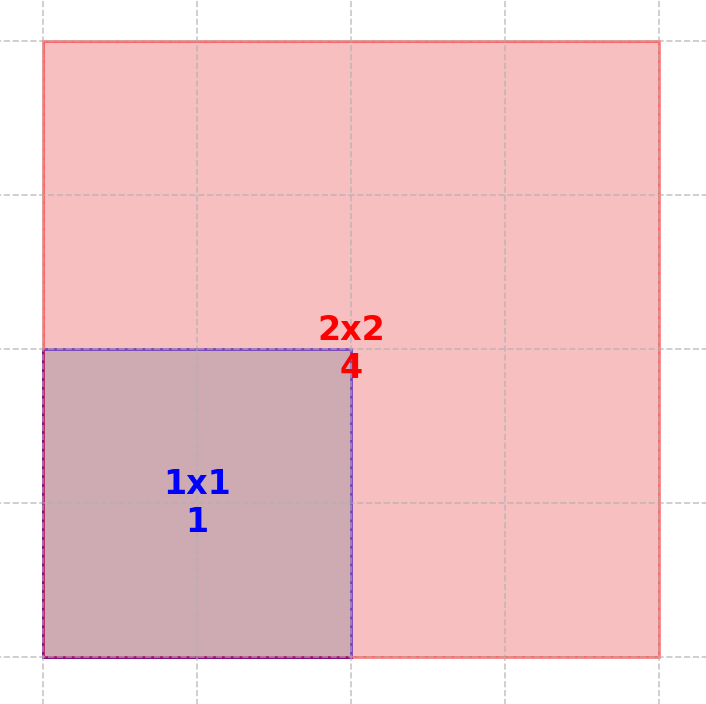
正方形の面積で二次関数をもっと身近に！

二次関数の理解を深めるためには、「二次的に増える」という感覚を掴むことが大切です。そこでおすすめなのが、正方形の一辺と面積の関係です。

• 一辺が 1cm の正方形の面積は 1 \times 1 = 1 \, \text{cm}^2
• 一辺が 2cm の正方形の面積は 2 \times 2 = 4 \, \text{cm}^2
• 一辺が 3cm の正方形の面積は 3 \times 3 = 9 \, \text{cm}^2

このように、一辺の長さが増えると面積はその「二乗」で増えていきます。この関係を通じて、お子さまは「二次的に増える」感覚を自然に理解できます。

実際に紙に正方形を描いて、辺の長さと面積の関係を確認してみましょう。視覚的に確認することで、二次関数の基本が自然に身に付くので、楽しく学べるはずです。

二次関数が将来にどう役立つか

中学生のお子さまにとって、二次関数は重要な単元の一つです。将来の職業においても、二次関数の考え方やグラフの理解は役に立ちます。例えば、エンジニアやデータ分析を行う職業では、数式のパターンやデータの変化を捉えるために二次関数の理解が必要です。また、日常生活で数値データを見たときに傾向を把握する力が身につき、将来的にデータを扱う力も育まれます。

自宅でお子さまの学習をサポートすることは大変ですが、二次関数の基礎を一緒に学んでいくことで、お子さまの学力向上につながります。ぜひ、一緒に楽しく取り組んでみてください！